In the past decade there have been rapid increases in the cruise industry, particularly in the number of passengers and cruise ships. As a result, many ports cannot keep up with this pace of development.
The biggest problem ports face is limited space to host ships, since constructing new berths is either impossible, expensive, or time-consuming. Moreover, crowded ports and destinations caused by the concentration of calls on certain days are a big concern.
These ports are asked to deal with improving the allocation of places for ships at port (quays or anchorage), known as the problem of berth allocation, which to date has yet to be addressed with a generally accepted methodology worldwide.
Therefore, the problems a port has to deal with are, on the one hand, the classification of places available based on various criteria and, on the other, the development of a methodology that is fair, transparent, and devoid of subjective criteria.
To achieve the above, a mathematical equation (algorithm) needs to be applied whereby the same data input yields the same output each time, which has to apply to all ports.
The equation that meets the above needs is:
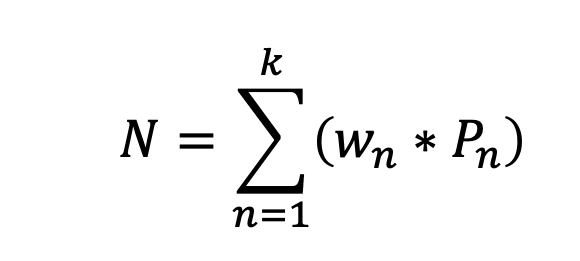
Where: N = grade, w= weight, P= parameter, k= amount of parameters
Although many people are concerned about using algorithms in such situations, this algorithm solves the berth allocation problem. That is not only because it has been successfully tested for many years in the port of Corfu, but most of all because it is beautiful.
In 1819, the British Romantic poet John Keats composed a poem titled “Ode on a Greek Urn”. The poem is famous, not least because of its last lines:
“Beauty is truth, truth beauty — that is all Ye know on earth, and all ye need to know.”
To the great theoretical physicist Paul Dirac what matters is not just any kind of beauty but mathematical beauty.
Αll great philosophers have mathematics as the foundation of their philosophy, and it is Pythagoras’s famous quote: “Number rules the Universe”.
In the forthcoming GA in Corfu, we will have the opportunity to talk more about the beauty of this algorithm, and not only this; there will be a little surprise!
Source: https://pressbooks.pub/simplydirac/chapter/mathematical-beauty/





